Mestre Panda

Dificuldade: média

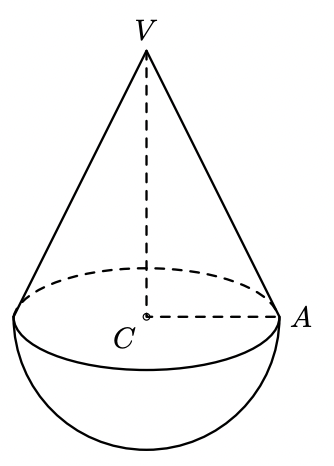
Na figura seguinte, está representado um sólido composto por um cone reto de vértice $V$ e uma semiesfera. A base do cone e a semiesfera têm centro no ponto $C$ e têm raio $\overline{A C}$.

Sabe-se que:

$\overline{A C}=6 \mathrm{~cm}$
$\overline{V A}=15 \mathrm{~cm}$

A figura não está desenhada à escala.

Determina o volume do sólido representado na figura.

Apresenta o resultado em centímetros cúbicos, arredondado às unidades.

Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, três casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2016, 1ª Fase - Grupo Exercício 877

Resumos

Resolução do Exercício:

Como a altura de um cone é perpendicular ao raio da base, o triângulo $[A C V]$ é retângulo em $C$. Logo podemos calcular $\overline{V C}$, recorrendo ao Teorema de Pitágoras:

$$\overline{V A}^{2}=\overline{V C}^{2}+\overline{A C}^{2} \Leftrightarrow 15^{2}=\overline{V C}^{2}+6^{2} \Leftrightarrow 225-36=\overline{V C}^{2} \Leftrightarrow 189=\overline{V C}_{\overline{V C}>0}^{2} \overline{V C}=\sqrt{189}$$

Assim, o volume do cone é:

$$V_{\text {cone }}=\frac{\text { Área da base } \times \text { altura }}{3}=\frac{\pi \times \overline{A C}^{2} \times \overline{V C}}{3}=\frac{\pi \times 6^{2} \times \sqrt{189}}{3} \approx 518,277 \mathrm{~cm}^{3}$$

O volume da semiesfera é:

$$V_{\text {semiesfera }}=\frac{V_{\text {esfera }}}{2}=\frac{\frac{4}{3} \pi \times \overline{A C}^{3}}{2}=\frac{4 \pi \times 6^{3}}{6} \approx 452,389 \mathrm{~cm}^{3}$$

Assim, o volume do sólido pode ser calculado como a soma dos volumes do cone e da semiesfera, pelo que, fazendo os cálculos e arredondando o resultado às unidades, vem:

$$V=V_{\text {cone }}+V_{\text {semiesfera }} \approx 518,277+452,389 \approx 971 \mathrm{~cm}^{3}$$

Fonte: Matemática? Absolutamente!

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Resolução do Exercício:

Comentários