Mestre Panda

Dificuldade: díficil

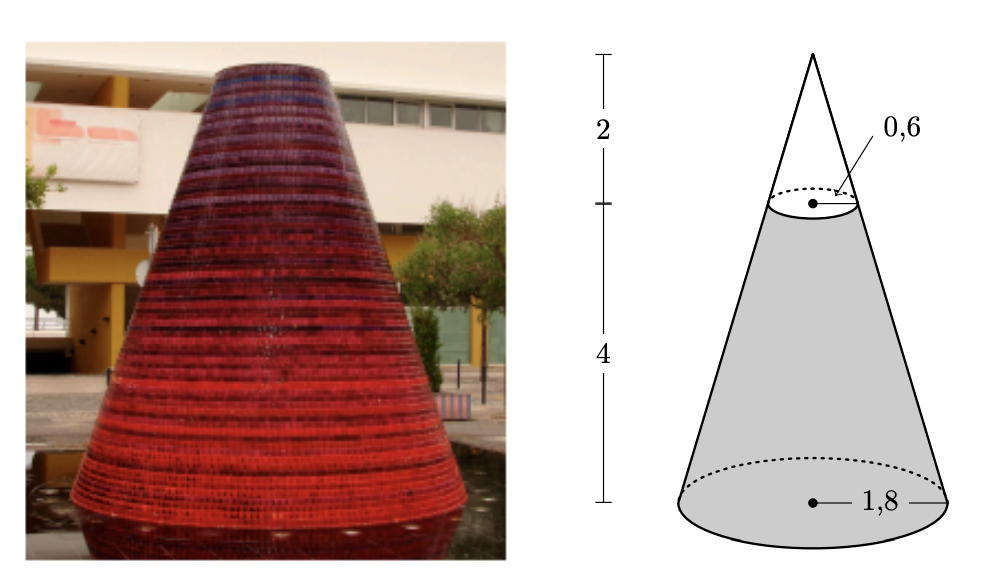
Na fotografia, à esquerda, podes observar um dos vulcões de água da Alameda dos Oceanos, no Parque das Nações, em Lisboa. Estes vulcões expelem, periodicamente, jatos de água. Na figura, à direita, está representado um cone de revolução.

A parte sombreada desta figura é um esquema do sólido que serviu de base à construção do vulcão de água.

As medidas de comprimento indicadas estão expressas em metros. 1,8 m, e 0,6 m são os comprimentos dos raios das duas circunferências.

A altura do cone é $6 \mathrm{~m}$

Determina, em metros cúbicos, o volume do sólido representado no esquema a sombreado. (Se a tua calculadora não possui a tecla $\pi$, utiliza o valor aproximado 3,14 ).

Indica o resultado arredondado às unidades e apresenta todos os cálculos que efetuares.

Sempre que, nos cálculos intermédios, procederes a arredondamentos, conserva duas casas decimais.

Fonte: Exame Matemática 3º Ciclo - 2006, 1ª Fase - Grupo Exercício 916

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários