Mestre Panda - Prepara-te para os Exames Nacionais

?

?

Cria conta para teres acesso a vídeos, estatísticas do teu progresso, exercícios originais e mais!

Exercício Anterior

Escolher Exercício

Próximo Exercício

Dificuldade: díficil

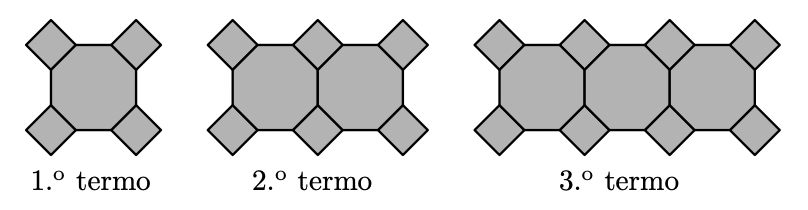
Na figura seguinte, estão representados os três primeiros termos de uma sequência de figuras constituídas por octógonos regulares, geometricamente iguais, e por quadrados.

O primeiro termo da sequência é composto por um octógono e por quatro quadrados. Cada um dos restantes termos obtém-se acrescentando ao termo anterior um octógono e dois quadrados.

Existe um termo desta sequência que tem exatamente 32 quadrados. Quantos octógonos tem esse termo?

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2022, 1ª Fase - Grupo Exercício 947

|

Exercício Anterior

Próximo Exercício

Comentários

Essandju Eric Rodrigues Mulangui

Criado em 04/05/2024 22:03

Não entendi a resolução.

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Ema Matos Essandju Eric Rodrigues Mulangui

Criado em 04/06/2024 16:10

n é o número total de octógonos. então 2n+2 é a fórmula necessária para descobrir os quadrados. Exemplo: 2x3+2=8

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.