Mestre Panda

Dificuldade: díficil

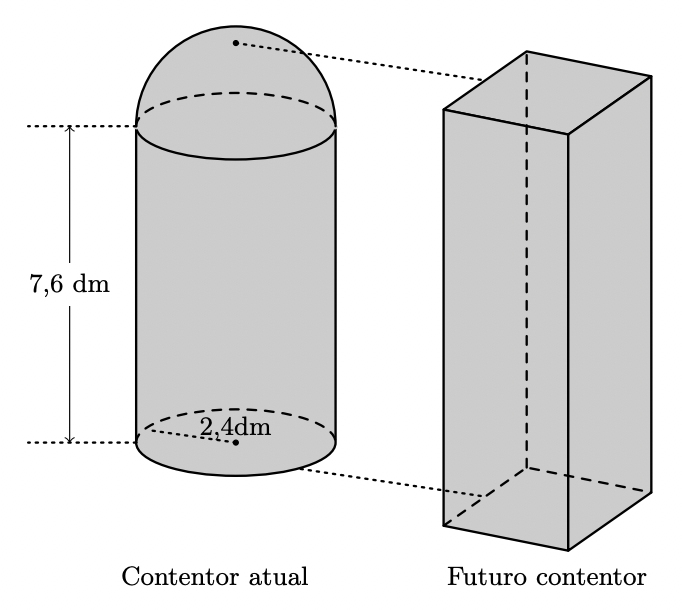
Os contentores de recolha seletiva de lixo de uma praia vão ser substituídos. O contentor atual tem a forma de um sólido que pode ser decomposto num cilindro e numa semiesfera com o mesmo raio, como se representa na figura seguinte.

O futuro contentor terá a forma de um prisma reto de bases quadradas, como também se representa na mesma figura.

Relativamente ao contentor atual, sabe-se que:

a altura do cilindro é $7,6 \mathrm{~dm}$;
o raio da base do cilindro é $2,4 \mathrm{~dm}$.

O futuro contentor terá o mesmo volume e a mesma altura do contentor atual.

Determina a medida da aresta da base do futuro contentor.

Apresenta o resultado em decímetros, arredondado às décimas. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, duas casas decimais.

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 870

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários