Mestre Panda

Dificuldade: díficil

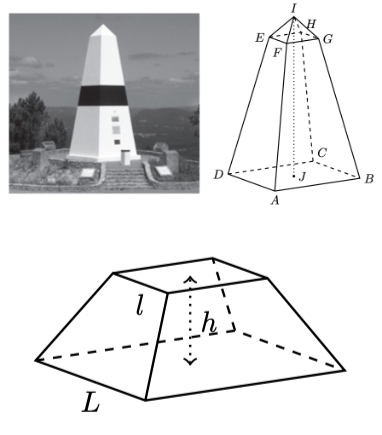
O centro geodésico de Portugal continental situa-se na Serra da Melriça, próximo de Vila de Rei. Nesse local, foi construído o marco geodésico que se pode observar na figura seguinte, à esquerda. Na figura da direita, está representado um modelo geométrico desse marco geodésico.

O modelo não está desenhado à escala.

O modelo do marco geodésico é um poliedro composto pelo tronco de pirâmide quadrangular regular $[A B C D E F G H]$ e pela pirâmide quadrangular regular $[E F G H I]$

O ponto $J$ é o centro do quadrado $[A B C D]$

Relativamente à figura da direita, sabe-se que:

$\overline{I J}=15 \mathrm{~cm}$
$\overline{A B}=8 \mathrm{~cm}$
$\overline{F G}=3 \mathrm{~cm}$
o volume da pirâmide $[E F G H I]$ é $6 \mathrm{~cm}^{3}$

Sabe-se ainda que o volume, $V$, de um tronco de pirâmide quadrangular regular é dado pela expressão $V=\frac{h}{3}\left(L^{2}+L \times l+l^{2}\right)$ em que:

$h$ é a altura do tronco de pirâmide;
$L$ é a aresta da base maior do tronco de pirâmide;
$l$ é a aresta da base menor do tronco de pirâmide.

Determina o volume do tronco de pirâmide $[A B C D E F G H]$

Sugestão: Começa por mostrar que a altura da pirâmide $[E F G H I]$ é igual a $2 \mathrm{~cm}$

Apresenta o resultado $\mathrm{em}^{3}$, arredondado às unidades. Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2015, 1ª Fase - Grupo Exercício 880

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários