Mestre Panda

Dificuldade: média

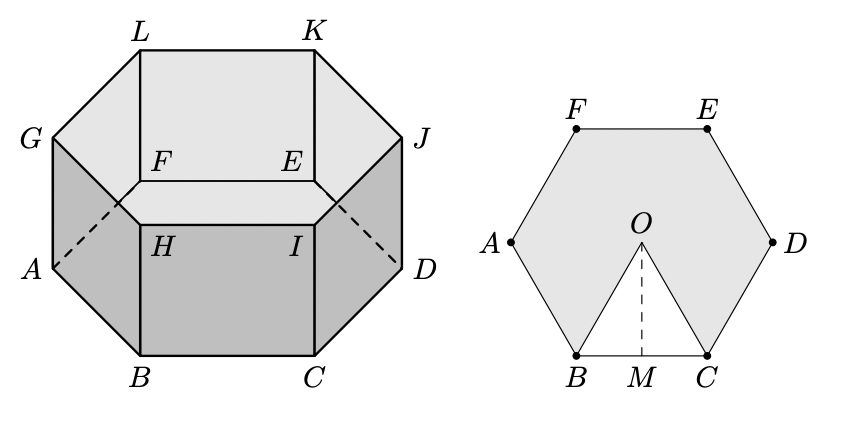
Na figura à esquerda está representado um esquema da piscina que a mãe da Marta comprou para colocar no jardim. A figura da direita representa um esquema da base da piscina.

Na figura da direita, $[A B C D E F G H I J K L]$ é um prisma regular e $\overline{B H}=1,5 \mathrm{~m}$

Na figura da esquerda, $[A B C D E F]$ é um hexágono, $\overline{B C}=2 \mathrm{~m}$ e $\overline{O M}=\sqrt{3}$ $\mathrm{m}$

Calcula, em metros cúbicos, a capacidade da piscina. Apresenta os cálculos que efetuares e, na tua resposta, escreve o resultado arredondado às décimas.

Nota: Sempre que, nos cálculos intermédios, procederes a arredondamentos, conserva três casas decimais.

Fonte: Exame Matemática 3º Ciclo - 2009, 1ª Fase - Grupo Exercício 907

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários