Mestre Panda

Dificuldade: díficil

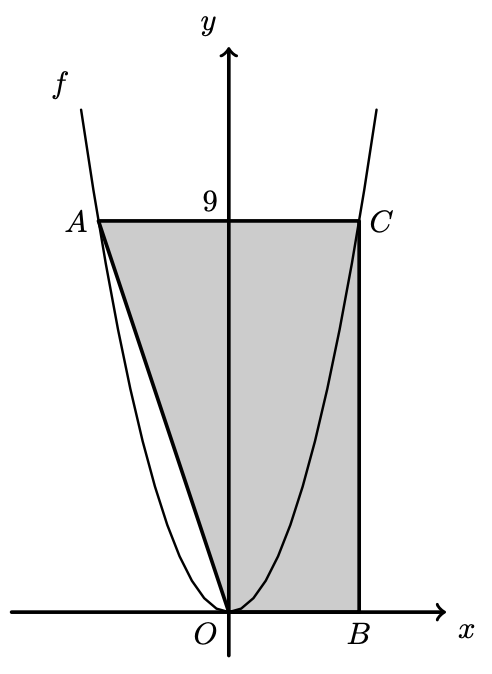
Na figura, estão representados, em referencial cartesiano, de origem no ponto $O$, parte do gráfico de uma função quadrática, $f$, e o trapézio $[A O B C]$.

Sabe-se que:

a função $f$ é definida por $f(x)=x^{2}$;
o ponto $A$ e o ponto $C$ pertencem ao gráfico da função $f$ e têm ordenada 9 ;
o ponto $B$ pertence ao eixo das abcissas e tem a mesma abcissa que o ponto $C$.

Determina a área do trapézio $[A O B C]$.

Apresenta o resultado na forma de dízima. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2022, 1ª Fase - Grupo Exercício 127

Resumos

Resolução do Exercício:

Como o ponto $C$ pertence ao gráfico da função $f$ e tem ordenada 9 , designando por $a$ a abcissa dos pontos $C$ e $B$, temos que:

$$f(a)=9 \Leftrightarrow a^{2}=9 \underset{a>0}{\Rightarrow} a=\sqrt{9} \Leftrightarrow a=3$$

Como os pontos $A$ e $C$ têm a mesma ordenada e pertencem ao gráfico da função $f$ (simétrico relativamente ao eixo $O y$ ) então têm ordenadas simétricas, pelo que a área do trapézio $[A O B C]$, na forma de dízima, é:

$$A_{[A O B C]}=\frac{\overline{A C}+\overline{O B}}{2} \times \overline{B C}=\frac{2 \times \overline{O B}+3}{2} \times 9=\frac{2 \times 3+3}{2} \times 9=\frac{9}{2} \times 9=\frac{81}{2}=40,5$$

Fonte: Matemática? Absolutamente!

Exercício Anterior

Próximo Exercício

Comentários

Carolina David

Criado em 10/06/2024 13:47

eu não percebi este exercício

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Leonor Mendonça Carolina David

Criado em 11/06/2024 00:15

Para calculares a área do trapézio precisas da altura, que é 9 (a ordenada de A e C) e da base menor e maior, que não sabes. Para calculares a base menor utilizas a função ( f(x)=2x2) e substituis f(x), que é a ordenada, pelo 9. O resultado da equação vai ser a base menor. Para calculares a base maior, é só fazeres o dobro da base menor. Por fim, como já tens todos os valores necessários, calculas a área da figura.

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Resolução do Exercício:

Comentários