Mestre Panda

Dificuldade: díficil

Numa Estação de Tratamento de Águas Residuais (ETAR), num determinado dia, foi registado o volume de água tratada, às 11 horas, às 13 horas e às 20 horas.

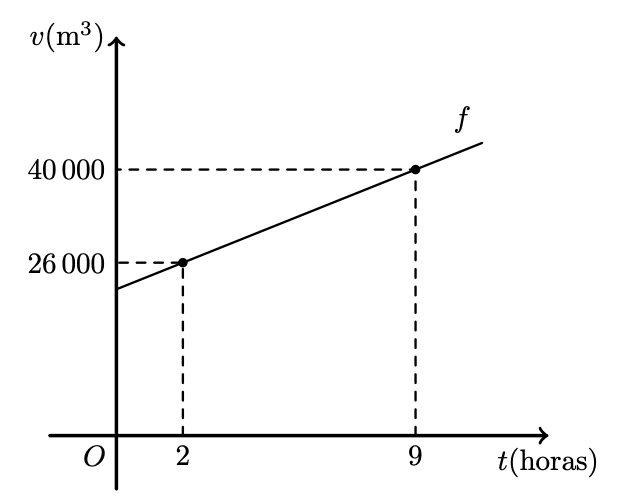
Com os valores registados, e considerando que o caudal de água tratada ao longo do dia foi constante, construiu-se o gráfico da figura ao lado, que traduz a correspondência entre o tempo $t$ (em horas), decorrido desde as 11 horas desse dia, e o volume de água tratada, $v$ (em metros cúbicos).

As 11 horas desse dia correspondem ao instante inicial (0 horas).

Qual foi o volume de água tratada registado às 11 horas desse dia?

Apresenta o resultado em metros cúbicos.

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2021, 1ª Fase - Grupo Exercício 656

Resumos

Resolução do Exercício:

Como o gráfico da função $f$ é parte de uma reta contém os pontos de coordenadas $(2,26000)$ e $(9,40000)$, então podemos calcular o valor do declive da reta:

$$m=\frac{40000-26000}{9-2}=\frac{14000}{7}=2000$$

Ou seja, a equação da reta é da forma:

$$y=2000 x+b$$

Substituindo as coordenadas de um ponto do gráfico, por exemplo $(2,26000)$, podemos determinar o valor da ordenada da origem $(b)$ :

$$26000=2000 \times 2+b \Leftrightarrow 26000=4000+b \Leftrightarrow 26000-4000=b \Leftrightarrow 22000=b$$

E assim, temos que a equação da reta é:

$$y=2000 x+22000$$

Desta forma o volume de água tratada registado às 11 horas, em metros cúbicos, corresponde a $f(0)$, ou seja, ao valor da ordenada na origem da reta:

$$f(0)=22000$$

Fonte: Matemática? Absolutamente!

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Resolução do Exercício:

Comentários