Mestre Panda

Dificuldade: díficil

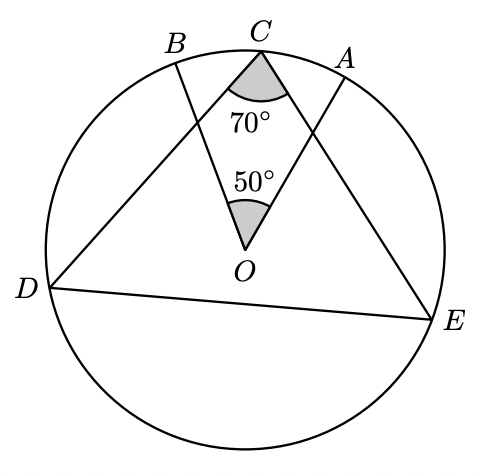
Na figura seguinte, está representada uma circunferência de centro $O$.

Os pontos $A, B, C, D$ e $E$ pertencem à circunferência.

Sabe-se que:

a amplitude do ângulo $A O B$ é $50^{\circ}$;
$\overline{C D}=\overline{C E}$;
$\overparen{B C}=\overparen{C A}$
a amplitude do ângulo $D C E$ é $70^{\circ}$.

A figura não está desenhada à escala.

Calcula a amplitude, em graus, do arco $B D$.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2023, 1ª Fase - Grupo Exercício 411

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Mauricio Lopes

Criado em 01/05/2024 19:50

Porque multiplicar o 2 por 70

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

renata dias Mauricio Lopes

Criado em 04/05/2024 14:38

porque não é um ângulo inscrito por isso para descobrir o arco DE é necessário multiplicar 0 70º por 2=140º, mas se for inscrito por exemplo o caso do 50º não é necessário e o arco BA corresponde a 50º, espero ter ajudado!

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Diego Basto Bastidas

Criado em 20/05/2024 17:42

eu calculei DE que dava 140 depois fui a 360 e tirei a soma de DE que é 140 e de BA que é 50 que ia dar 360-190 que é 170 depois a esses 170 dividi por dois que da os 85

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Valentina López

Criado em 15/06/2025 13:27

Eu fiz o ângulo CED (180-70 e depois a dividir por 2 já que os segmentos de reta DC e CE são iguais), depois o arco DC menos o arco BC (o arco BC é 50:2 pois os arcos BC e BA são iguais)

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários