Mestre Panda

Dificuldade: díficil

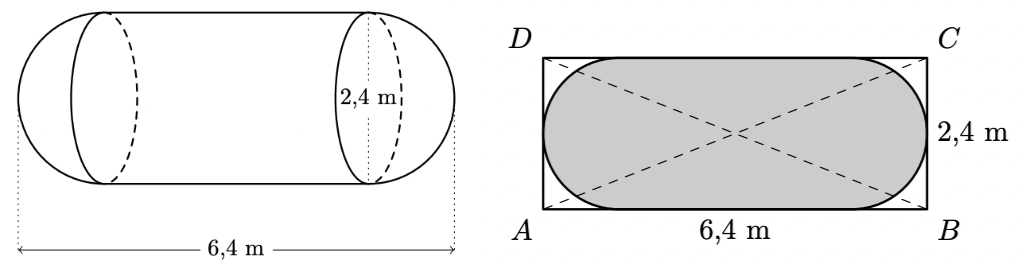
Uma cisterna tem a forma de um sólido que pode ser decomposto num cilindro e em duas semiesferas, como se vê na figura à esquerda.

De acordo com a figura:

o comprimento da cisterna é $6,4 \mathrm{~m}$;
o diâmetro da base do cilindro é $2,4 \mathrm{~m}$;
as bases do cilindro e as semiesferas têm o mesmo diâmetro. A figura não está desenhada à escala.

A cisterna é colocada sobre a plataforma do reboque de um camião.

Essa plataforma tem a forma de um retângulo com largura igual ao diâmetro da base do cilindro e comprimento igual ao da cisterna.

Para sustentar a cisterna, a plataforma do camião foi reforçada com duas barras metálicas, coincidindo com as suas diagonais, representadas na figura por $[A C]$ e $[B D]$.

A figura não está desenhada à escala.

Determina o comprimento da barra representada por $[A C]$.

Apresenta o resultado, em metros, arredondado às décimas. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 771

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários