Mestre Panda

Dificuldade: díficil

No telhado de uma casa, existe um painel solar incorporado numa peça metálica. O painel e a peça, em conjunto, têm a forma de um prisma triangular reto cujas bases são triângulos retângulos.

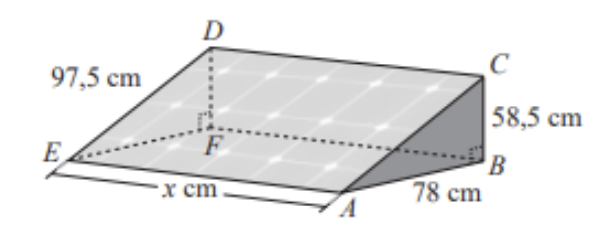
Na figura seguinte, está representado o prisma triangular reto $[A B C D E F]$, modelo da peça metálica. Os segmentos de reta $[E F]$ e $[A B]$ são perpendiculares aos segmentos de reta $[D F]$ e $[B C]$, respetivamente.

A figura não está desenhada à escala.

Na figura, o painel solar está representado pelo retângulo $[A C D E]$. As medidas da peça metálica são as indicadas na figura: $\overline{A B}=78 \mathrm{~cm}, \overline{B C}=58,5 \mathrm{~cm}, \overline{D E}=97,5 \mathrm{~cm}$ e $\overline{A E}=x \mathrm{~cm}(x>0)$.

Admite que o volume do prisma $[A B C D E F]$ é $445000 \mathrm{~cm}^{3}$.

Determina a área do painel solar.

Apresenta o resultado $\mathrm{em}^{2}$, arredondado às unidades. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 868

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários