Mestre Panda

Dificuldade: média

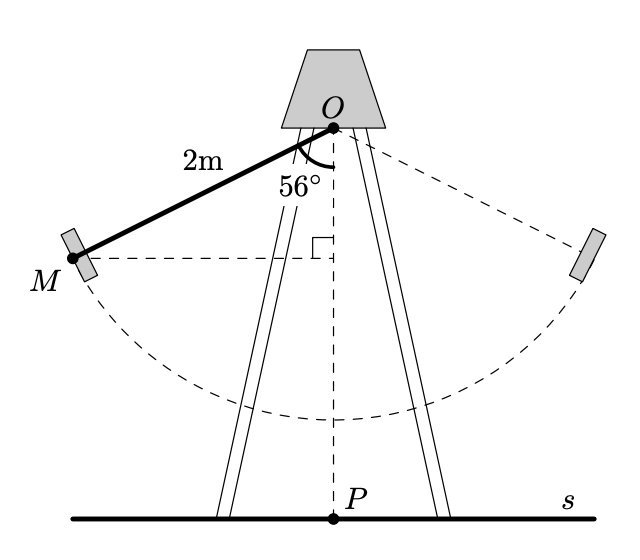
Na figura seguinte, está representado um esquema de um baloiço num instante em que a cadeira do baloiço se encontra na posição assinalada com o ponto $M$.

No esquema, o segmento de reta $[O M]$ representa o cabo do baloiço e a reta $s$ representa o solo.

Sabe-se que:

o ponto $P$ é o pé da perpendicular traçada do ponto $O$ para a reta $s$;
o ponto $N$ é o pé da perpendicular traçada do ponto $M$ para a reta $O P$;
$M \hat{O} N=56^{\circ}$;
$\overline{O M}=2 \mathrm{~m} ;$
$\overline{O P}=2,5 \mathrm{~m}$.

A figura não está desenhada à escala.

Determina $\overline{N P}$, ou seja, determina a distância da cadeira ao solo quando esta se encontra no ponto

Apresenta o valor pedido em metros, arredondado às centésimas. Se procederes a arredondamentos nos cálculos intermédios, conserva pelo menos três casas decimais.

Apresenta todos os cálculos que efetuares.

Sugestão : começa por determinar $\overline{O N}$.

Fonte: Exame Matemática 3º Ciclo - 2017, 1ª Fase - Grupo Exercício 92

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários