Mestre Panda

Dificuldade: díficil

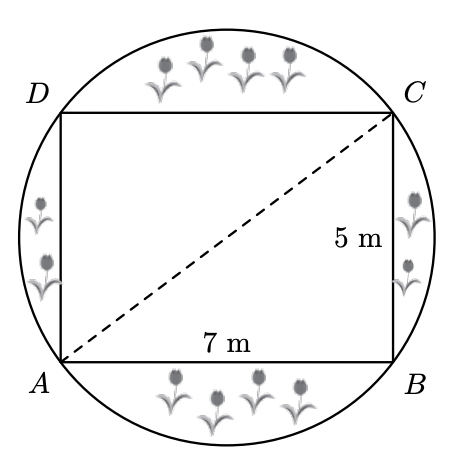
Na figura seguinte, está representado o círculo de diâmetro $[A C]$, modelo de um canteiro de um jardim. Nesse canteiro, foram plantadas tulipas, exceto na zona representada pelo retângulo $[A B C D]$, cujos vértices pertencem à circunferência que delimita o círculo.

Sabe-se que $\overline{A B}=7 \mathrm{~m}$ e $\overline{B C}=5 \mathrm{~m}$.

A figura não está desenhada à escala.

Qual é a área da zona do canteiro onde foram plantadas tulipas?

Apresenta o resultado, em metros quadrados, arredondado às unidades. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, duas casas decimais.

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2021, 1ª Fase - Grupo Exercício 768

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários