Mestre Panda - Prepara-te para os Exames Nacionais

Dificuldade: díficil

Mostrar Texto/Figura do Grupo

Um saco contém várias bolas com o número 1, várias bolas com o número 2 e várias bolas com o número 3.

As bolas são indistinguíveis ao tato.

A Maria realizou dez vezes o seguinte procedimento: retirou, ao acaso, uma bola do saco, registou o número inscrito na bola e colocou novamente a bola no saco.

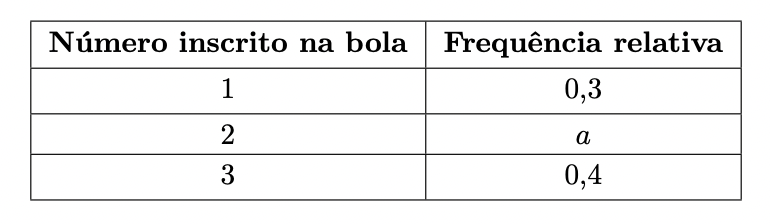
Em seguida, a Maria calculou a frequência relativa de cada um dos números 1,2 e 3 e elaborou uma tabela.

Nessa tabela, substituiu-se a frequência relativa do número 2 por a, obtendo-se a tabela em baixo.

Admite que, no saco, metade das bolas têm o número 1.

Admite ainda que se vai retirar uma bola do saco um milhão de vezes, seguindo o procedimento da Maria.

Será de esperar que a frequência relativa do número 1 se mantenha igual a 0,3 ?

Justifica a tua resposta.

Fonte: Prova Final 3º Ciclo – 2012, 2ª fase

Resumos

Resolução do Exercício:

Não. Quando se repete muitas vezes uma experiência aleatória, a frequência relativa de uma observação tende a aproximar-se da probabilidade de acontecer essa observação.

Assim, se repetirmos o procedimento da Maria um milhão de vezes, e metade das bolas no saco tem o número 1 , é expectável que a frequência relativa do número 1 se aproxime muito de 0,5

Fonte: Matemática? Absolutamente!

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Resolução do Exercício:

Comentários