Mestre Panda

Dificuldade: média

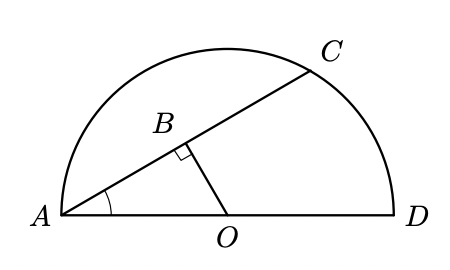
Na figura seguinte, está representada uma semicircunferência de centro no ponto $O$ e diâmetro $[A D]$

Sabe-se que:

ponto $C$ pertence à semicircunferência;
o ponto $\mathrm{B}$ pertence à corda $[A C]$
o triângulo $[A B O]$ é retângulo em $B$
$\overline{O B}=1 \mathrm{~cm}$
$B \hat{A} O=25^{\circ}$

A figura não está desenhada à escala.

Qual é a amplitude, em graus, do arco $A C$ ?

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2015, 1ª Fase - Grupo Exercício 428

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Sky0_0land Eliane

Criado em 14/05/2025 18:15

quando posso saber se no meu calculo esta certo? tipo eu depois dividi o 130 por 2 que deu 65, mas ainda nao entendi porque foi 130

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Rodrigo Taborda Sky0_0land Eliane

Criado em 18/06/2025 18:08

A amplitude do arco de uma semicircunferência é sempre 180º (porque 180x2 = 360º). Se o ângulo BAO tem 25º, o seu arco terá 50º (porque está inscrito na circunferência e não é um ângulo ao centro, ou seja CD=25x2=50º). Como AD=180º (já que é semicircunferência) e CD=50º, AC será a diferença entre os arcos AD e CD. Por isso, AC= AD-CD. Substituindo os valores, AC=180-50=130.

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários