Mestre Panda

Dificuldade: média

Mostrar Enunciado do Grupo

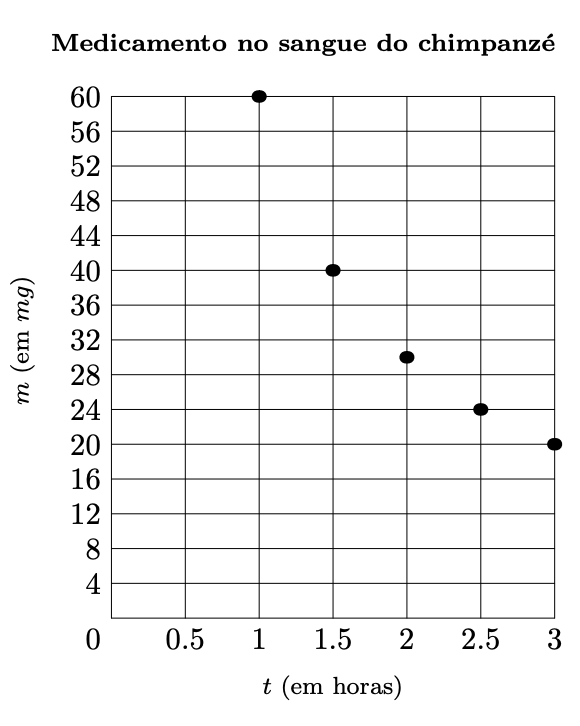
Administrou-se um medicamento a um chimpanzé doente. Uma hora depois, mediu-se a massa, em miligramas, de medicamento existente no sangue do chimpanzé. Repetiu-se, de meia em meia hora, essa medição.

Cada um dos pontos representados no referencial da figura ao lado corresponde a uma medição. Observando esses pontos, podemos saber a massa, $m$, em miligramas, de medicamento existente no sangue do chimpanzé, em cada um dos instantes em que as medições foram feitas.

No referencial, $t$ designa o tempo, em horas, decorrido desde o instante em que se administrou o medicamento.

Questão:

Tal como os valores obtidos nas medições sugerem, tem-se que, para $1 \leq t \leq 3$, a massa de medicamento existente no sangue do chimpanzé e o tempo são grandezas inversamente proporcionais.

Qual é, nestas condições, a constante de proporcionalidade?

Fonte: Exame Matemática 3º Ciclo - 2010, 1ª Fase - Grupo Exercício 284

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Questão:

Escreve a tua resposta aqui:

Comentários