Mestre Panda

Dificuldade: média

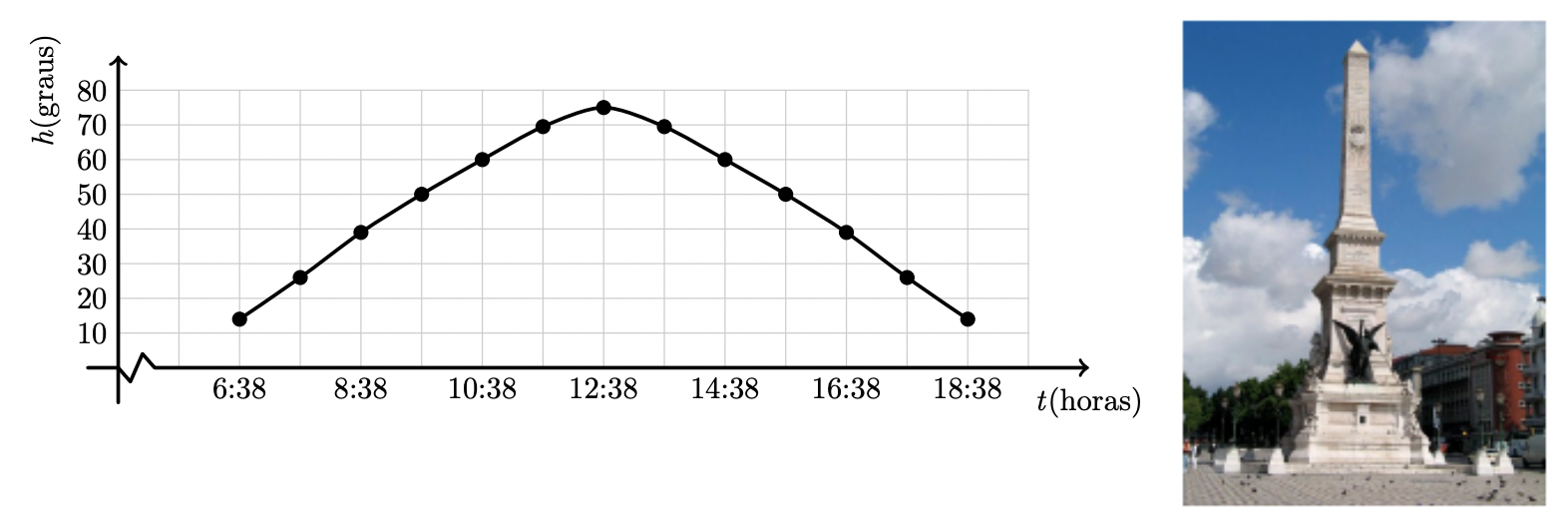
A altura, $h$, do Sol é a amplitude, medida em graus, do ângulo que os raios solares fazem com o plano do horizonte.

O gráfico seguinte dá a altura do Sol às horas do dia 21 de junho de 2006, solstício de Verão, na região de Lisboa, de acordo com os dados do Observatório Astronómico de Lisboa.

A fotografia da direita é a do monumento da praça dos Restauradores, em Lisboa.

A altura desse monumento é de 30 metros.

No dia 21 de junho de 2006, às 15 horas e 38 minutos, qual foi, em metros, o comprimento da sombra projetada no chão pelo monumento?

Começa por fazer um esboço que ilustre a situação. Indica o resultado arredondado às unidades e apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2006, 1ª Fase - Grupo Exercício 121

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários