Mestre Panda

Dificuldade: díficil

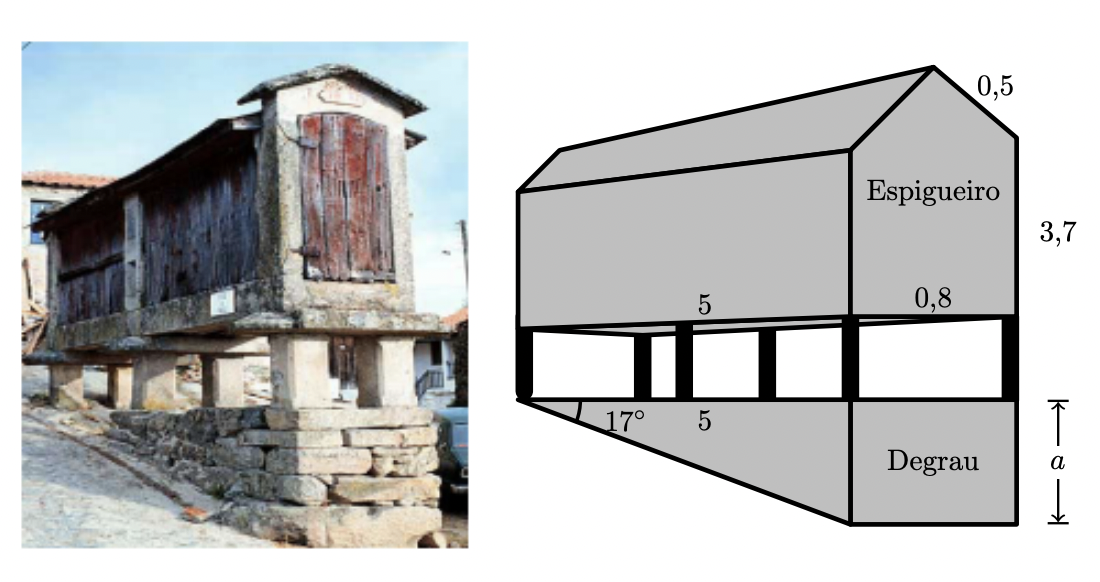
Os espigueiros são construções que servem para guardar cereais, ao mesmo tempo que os protegem da humidade e dos roedores. Por isso, são construídos sobre estacas (pés do espigueiro), de forma que não estejam em contacto direto com o solo.

Se o terreno for inclinado, os pés do espigueiro assentam num, para que o degrau espigueiro fique na horizontal, como mostra a fotografia (na figura seguinte, à esquerda).

A figura da direita é um esquema do espigueiro da fotografia. Neste esquema, estão também representados os seis pés do espigueiro, bem como o degrau no qual eles assentam. O esquema não está desenhado à escala. As medidas de comprimento indicadas estão expressas em metros. A questão seguinte refere-se a este esquema.

O espigueiro é um prisma pentagonal reto, cujas bases são pentágonos não regulares. Cada pentágono pode ser decomposto num retângulo e num triângulo isósceles.

Determina (em metros cúbicos) o volume do espigueiro.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2005, 1ª Fase - Grupo Exercício 917

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários