Mestre Panda

Dificuldade: díficil

O Palácio Nacional da Pena está situado em Sintra. Em julho de 2007, foi eleito uma das Sete Maravilhas de Portugal.

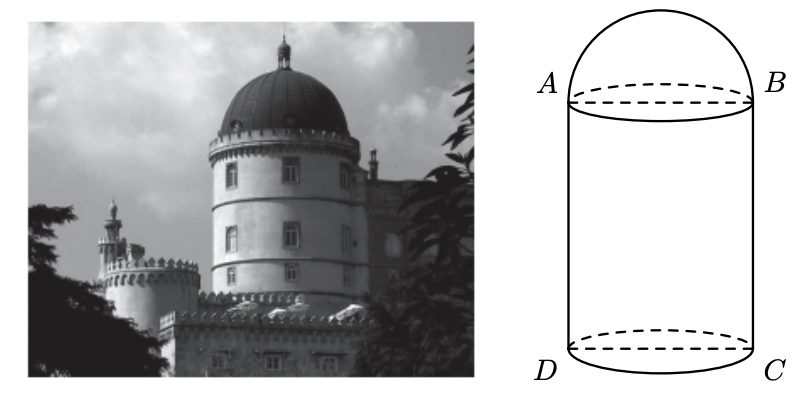
A figura da direita é uma fotografia de uma das torres desse palácio. Na figura da esquerda, está representado um modelo geométrico dessa torre.

O modelo não está desenhado à escala. O modelo representado na figura da direita é um sólido que pode ser decomposto num cilindro e numa semiesfera.

Sabe-se que:

os pontos $A, B, C$ e $D$ são os vértices de um retângulo
o raio da base do cilindro é igual ao raio da semiesfera e é igual a $3 \mathrm{~cm}$
o volume total do sólido é igual a $285 \mathrm{~cm}^{3}$

Determina a altura do cilindro.

Apresenta o resultado em centímetros, arredondado às décimas. Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2015, 1ª Fase - Grupo Exercício 882

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários