Mestre Panda

Dificuldade: média

Para determinar a altura $(h)$ de uma antena cilíndrica, o Paulo aplicou o que aprendeu nas aulas de Matemática, porque não conseguia chegar ao ponto mais alto dessa antena.

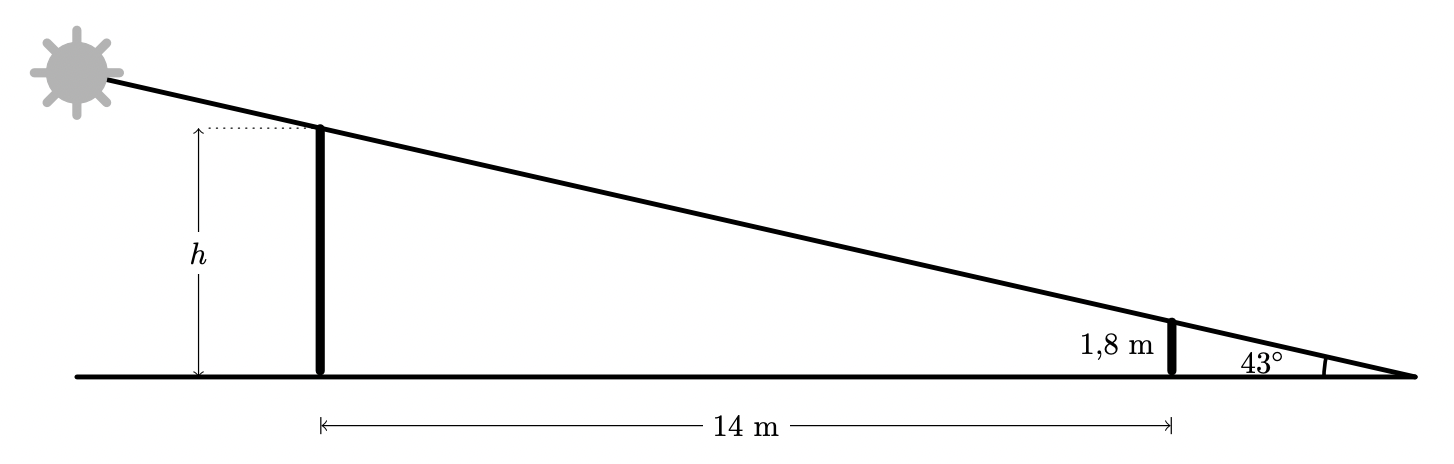
No momento em que a amplitude do ângulo que os raios solares faziam com o chão era de $43^{\circ}$, parte da sombra da antena estava projetada sobre um terreno irregular e, por isso, não podia ser medida.

Nesse instante, o Paulo colocou uma vara perpendicularmente ao chão, de forma que as extremidades das sombras da vara e da antena coincidissem. A vara, com $1,8 \mathrm{~m}$ de altura, estava a $14 \mathrm{~m}$ de distância da antena.

Na figura seguinte, que não está desenhada à escala, podes ver um esquema que pretende ilustrar a situação descrita.

Qual é a altura $(h)$ da antena?

Na tua resposta, indica o resultado arredondado às unidades e a unidade de medida.

Apresenta todos os cálculos que efetuares.

Sempre que, nos cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Fonte: Exame Matemática 3º Ciclo - 2007, 1ª Fase - Grupo Exercício 119

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários