Mestre Panda

Dificuldade: média

Em algumas pontes, os candeeiros de iluminação pública estão inclinados em relação ao plano do tabuleiro da ponte, para reduzir a luz projetada sobre os rios. Na ponte Vasco da Gama, os candeeiros foram instalados desse modo, conforme se pode observar na figura seguinte, à direita.

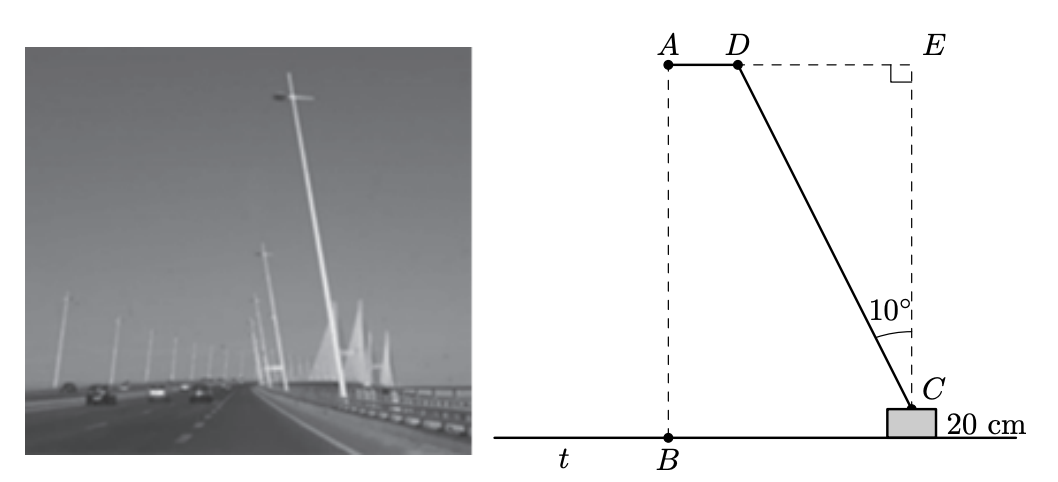
Na figura à esquerda, apresenta-se, em esquema, um candeeiro desse tipo, instalado numa outra ponte. Este candeeiro é constituído por duas peças, representadas na figura pelos segmentos de reta $[A D]$ e $[C D]$

Relativamente ao esquema da direita,

a reta $t$ representa o tabuleiro da ponte;
o ponto $A$ representa a lâmpada, e o ponto $B$ é o pé da perpendicular traçada do ponto $A$ para a reta $t$;
o segmento de reta $[A D]$ é perpendicular ao segmento de reta $[A B]$;
o poste do candeeiro é representado pelo segmento de reta $[C D]$ e tem $4,1 \mathrm{~m}$ de comprimento;
$D \hat{C} E=10^{\circ}$, sendo a reta $C E$ perpendicular à reta $t$;
a distância do ponto $C$ à reta $t$ é igual a $20 \mathrm{~cm}$.

A figura não está desenhada à escala.

Determina $\overline{A B}$, ou seja, determina a distância da lâmpada do candeeiro ao tabuleiro da ponte.

Apresenta o valor pedido em metros, arredondado às décimas.

Se procederes a arredondamentos nos cálculos intermédios, conserva pelo menos três casas decimais. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2017, 1ª Fase - Grupo Exercício 94

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários