Mestre Panda

Dificuldade: díficil

O Aqueduto das Águas Livres é um sistema de abastecimento de água à cidade de Lisboa, construído no século XVIII. Ao longo do seu percurso, existem várias claraboias. A figura à esquerda é uma fotografia de uma dessas claraboias.

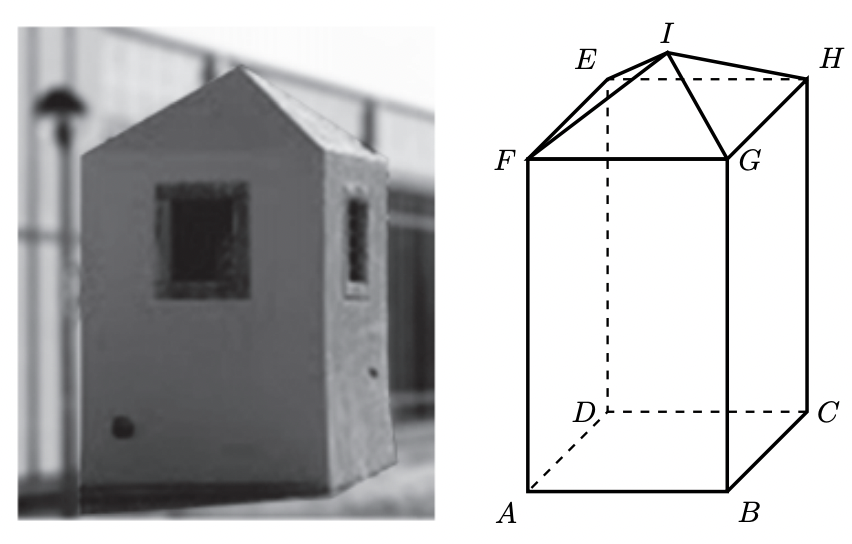
Na figura da direita, está representado um modelo geométrico dessa claraboia.

O modelo representado na figura da direita é um sólido que pode ser decomposto no prisma quadrangular regular $[A B C D E F G H]$, de base $[A B C D]$, e na pirâmide quadrangular regular $[E F G H I]$.

O modelo não está desenhado à escala.

Seja $V$ o volume do prisma $[A B C D E F G H]$ e seja $V^{\prime}$ o volume da pirâmide $[E F G H I]$ Admite que a altura da pirâmide é a quarta parte da altura do prisma.

Qual é o valor do quociente $\frac{V^{\prime}}{V} ?$

Fonte: Exame Matemática 3º Ciclo - 2014, 1ª Fase - Grupo Exercício 885

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários