Mestre Panda

Dificuldade: média

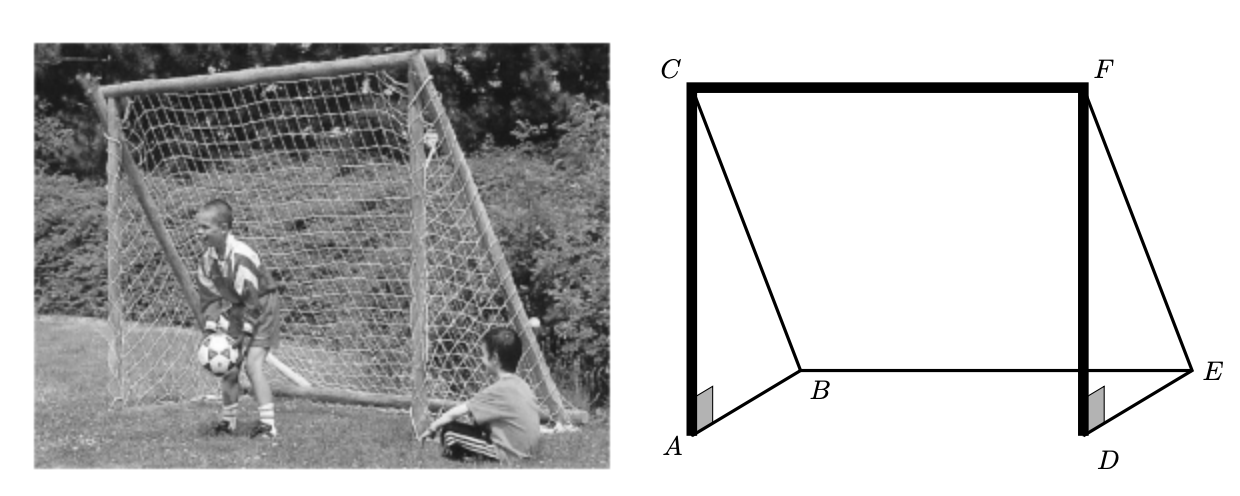
No jardim do clube desportivo Os Medalhados, existem duas balizas como a representada na figura seguinte, à esquerda.

A figura à direita representa um esquema da baliza da figura da esquerda. Os triângulos $[A B C]$ e $[D E F]$ são retângulos em $A$ e em $D$, respetivamente. $[B E F C]$ é um retângulo.

Nota: a figura da direita não está desenhada à escala.

Sabe-se que: $\overline{A B}=120 \mathrm{~cm}, \overline{B E}=180 \mathrm{~cm}$ e $\overline{A C}=160 \mathrm{~cm}$.

Determina a área do retângulo $[B E F C]$ do esquema da baliza representada na figura da direita. Apresenta os cálculos que efetuares e, na tua resposta, escreve a unidade de medida.

Fonte: Exame Matemática 3º Ciclo - 2009, 1ª Fase - Grupo Exercício 805

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários