Mestre Panda - Prepara-te para os Exames Nacionais

?

?

Cria conta para teres acesso a vídeos, estatísticas do teu progresso, exercícios originais e mais!

Exercício Anterior

Escolher Exercício

Próximo Exercício

Dificuldade: díficil

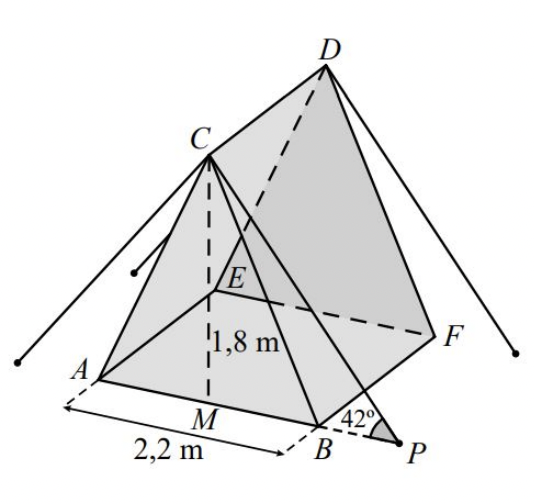
Na figura seguinte, está representado um modelo de uma tenda de campismo, montada numa superfície plana, com os cabos de suporte que a fixam a essa superfície.

No modelo, o prisma triangular reto $[A B C D E F]$ representa a tenda, o triângulo $[A B C]$ representa a entrada da tenda, o segmento de reta $[C P]$ representa um dos cabos de suporte, e o ponto $P$ representa o local da superfície onde a estaca fixa esse cabo.

Relativamente ao modelo, sabe-se que:

o triângulo $[A B C]$ é isósceles e $\overline{A C}=\overline{B C}$;
$M$ é o ponto médio de $[A B]$ e $P$ pertence à reta $A B$;
$\overline{A B}=2,2 \mathrm{~m} \mathrm{~e~} \overline{C M}=1,8 \mathrm{~m}$;
$C \hat{P} M=42^{\circ}$.

O modelo não está desenhado à escala.

Calcula $\overline{B C}$, utilizando o teorema de Pitágoras.

Apresenta o resultado em metros, arredondado às unidades. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2023, 1ª Fase - Grupo Exercício 764

|

Exercício Anterior

Próximo Exercício

Comentários

Lara Brandão

Criado em 10/06/2024 14:09

Uma ajuda: em primeiro determinem MB

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.