Mestre Panda

Dificuldade: média

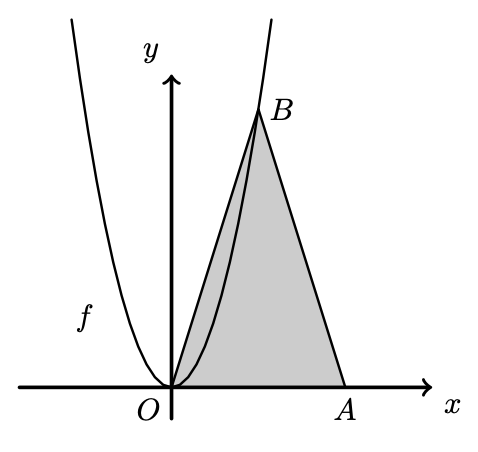
Na figura seguinte, estão representados, em referencial cartesiano, uma função quadrática $f$ e o triângulo isósceles $[O A B]$

Sabe-se que:

o ponto $O$ é a origem do referencial;
o ponto $A$ tem coordenadas $(4,0)$;
o ponto $B$ é um ponto do gráfico de $f$;
$\overline{O B}=\overline{A B}$;
a função $f$ é definida por $f(x)=4 x^{2}$

Determina a área do triângulo $[O A B]$

Mostra como chegaste à tua resposta.

Fonte: Exame Matemática 3º Ciclo - 2017, 1ª Fase - Grupo Exercício 132

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Fabiana Caunde

Criado em 08/06/2024 15:05

De onde veio o 2 do yb?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Haidé Parchão Fabiana Caunde

Criado em 08/06/2024 22:03

Pois, eu tbm n sei

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Raquel Campos Fabiana Caunde

Criado em 09/06/2024 15:58

como o triângulo é isósceles, o lado BO e BA têm o msm comprimento. então, o ponto B pertence à mediatriz do segmento OA Ou seja, a mediatriz indica a metade do segmento. O segmento tem 4 de comprimento, logo, o ponto B vai ter de abcissa 2, porque o ponto B faz parte da mediatriz do segmento Agora é substituir o x por 2 na expressão da função, obtendo o valor do y do ponto B, que é o valor da altura do triângulo. Espero ter ajudado :)

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Fabiana Caunde Raquel Campos

Criado em 09/06/2024 22:41

Ajudou muito, obrigada!

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Rahnia Adão

Criado em 10/06/2024 00:08

A altura não é 64?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Raquel Campos Rahnia Adão

Criado em 10/06/2024 11:59

Não, porque ao saber que o ponto B tem 2 como valor no eixo das abcissas, substituímos o x por 2 na expressão da função. ou seja f(x)=4x². Se substituirmos o x por 2 vai ficar: f(2)=4*2²<=> f(2)=4*4 <=> f(2)=16 16 é o valor de y do ponto B, ou seja a altura do triângulo

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Rahnia Adão Raquel Campos

Criado em 10/06/2024 21:44

Como descobriu o 2?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Rahnia Adão

Criado em 10/06/2024 21:44

Como descobriu o 2?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Beatriz Ferreira Rahnia Adão

Criado em 11/06/2024 10:08

Raquel Campos: "como o triângulo é isósceles, o lado BO e BA têm o msm comprimento. então, o ponto B pertence à mediatriz do segmento OA Ou seja, a mediatriz indica a metade do segmento. O segmento tem 4 de comprimento, logo, o ponto B vai ter de abcissa 2, porque o ponto B faz parte da mediatriz do segmento Agora é substituir o x por 2 na expressão da função, obtendo o valor do y do ponto B, que é o valor da altura do triângulo. Espero ter ajudado :)"

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Raquel Campos Rahnia Adão

Criado em 11/06/2024 11:24

Como o triângulo é isósceles, então o ponto B está à mesma distância dos pontos A e O. Então ele pertence à mediatriz do segmento de reta AO. A mediatriz é uma reta que passa pelo ponto médio de um segmento de reta, de forma perpendicular. Ou seja, se B pertence à reta que determina a metade de AO, então o ponto B vai ter de abcissa metade do comprimento de AO, ou seja 4/2=2

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários