Mestre Panda

Dificuldade: díficil

No telhado de uma casa, existe um painel solar incorporado numa peça metálica. O painel e a peça, em conjunto, têm a forma de um prisma triangular reto cujas bases são triângulos retângulos.

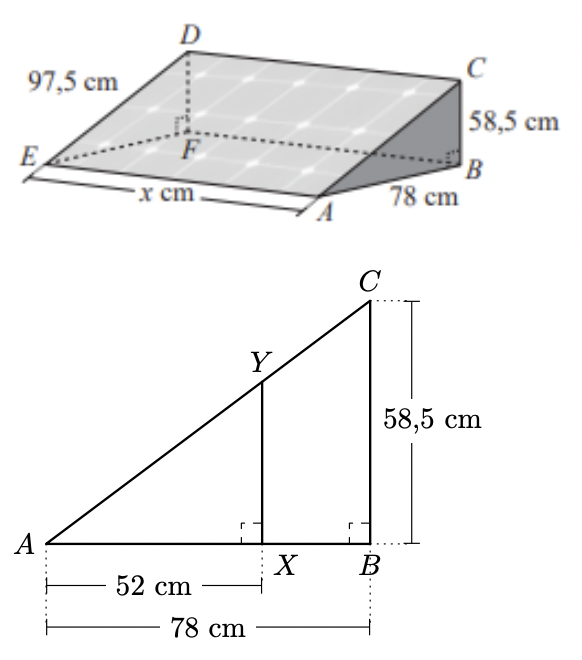
Na figura de cima, está representado o prisma triangular reto $[A B C D E F]$, modelo da peça metálica. Os segmentos de reta $[E F]$ e $[A B]$ são perpendiculares aos segmentos de reta $[D F]$ e $[B C]$, respetivamente.

A figura não está desenhada à escala.

Na figura de baixo, está representada uma das bases do prisma triangular reto $[A B C D E F]$, modelo da peça metálica.

A peça metálica tem uma haste de reforço, representada na figura por $[X Y]$.

De acordo com a figura:

o ponto $X$ pertence a $[A B]$ e o ponto $Y$ pertence a $[A C]$;
as retas $X Y$ e $A B$ são perpendiculares;
$\overline{A B}=78 \mathrm{~cm}, \overline{B C}=58,5 \mathrm{~cm}$ e $\overline{A X}=52 \mathrm{~cm}$.

Determina o comprimento da haste, ou seja, $\overline{X Y}$.

Apresenta o resultado em centímetros. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 1028

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários