Mestre Panda

Dificuldade: díficil

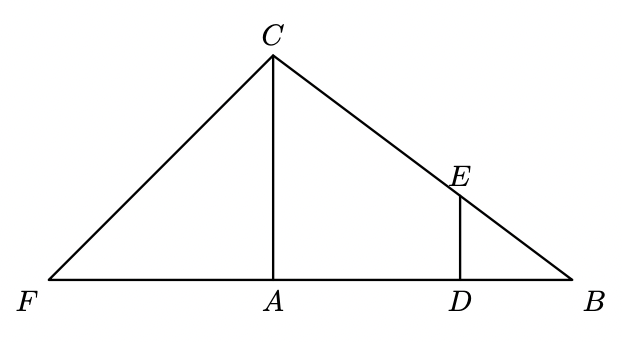
Relativamente à figura seguinte, sabe-se que:

os triângulos $[A B C]$ e $[A F C]$ são retângulos em $A$
o triângulo $[A F C]$ é isósceles
o ponto $E$ pertence ao segmento de reta $[B C]$
o ponto $D$ pertence ao segmento de reta $[A B]$
os segmentos de reta $[A C]$ e $[D E]$ são paralelos
$\overline{A C}=12 \mathrm{~cm}$
o perímetro do triângulo $[A B C]$ é $48 \mathrm{~cm}$
o perímetro do triângulo $[D B E]$ é $16 \mathrm{~cm}$

Nota - A figura não está desenhada à escala.

Determina o comprimento da circunferência que passa nos pontos $A, F$ e $C$

Apresenta o resultado em centímetros, arredondado às unidades. Apresenta os cálculos que efetuares.

Nota - Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Fonte: Exame Matemática 3º Ciclo - 2012, 1ª Fase - Grupo Exercício 790

Resumos

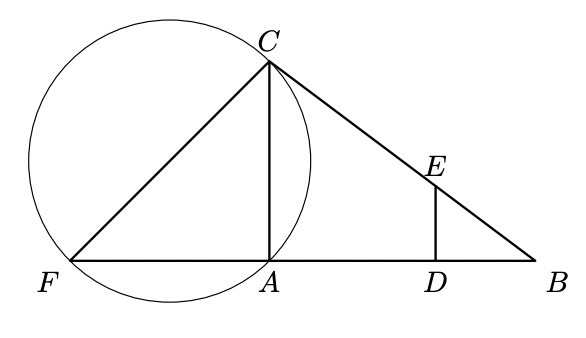
Resolução do Exercício:

Como o triângulo $[A F C]$ é retângulo em $A$, então o lado $[F C]$ é um diâmetro da circunferência que passa nos pontos $A, F$ e $C$

Temos ainda que $\overline{A C}=12 \mathrm{~cm}$ e que o triângulo $[A F C]$ é isósceles, pelo que também $\overline{A F}=12 \mathrm{~cm}$, e recorrendo ao Teorema de Pitágoras podemos determinar a medida do segmento $[F C]$ :

$$\begin{gathered}\overline{F C}^{2}=\overline{A C}^{2}+\overline{A F}^{2} \Leftrightarrow \overline{F C}^{2}=12^{2}+12^{2} \Leftrightarrow \\Leftrightarrow \overline{F C}^{2}=144+144 \Leftrightarrow \overline{F C}^{2}=288 \underset{BC>0} {\Rightarrow} \Rightarrow \overline{F C}=\sqrt{288}\end{gathered}$$

Assim, temos que o raio circunferência é $r=\frac{\sqrt{288}}{2}$, pelo que o comprimento da circunferência em centímetros, arredondado às unidades, é

$$P_{\circ}=2 \pi r=2 \pi \times \frac{\sqrt{288}}{2}=\pi \times \sqrt{288} \approx 53 \mathrm{~cm}$$

Fonte: Matemática? Absolutamente!

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Resolução do Exercício:

Comentários