Mestre Panda

Dificuldade: média

Em São Torpes, no concelho de Sines, encontra-se uma central termoelétrica com duas chaminés.

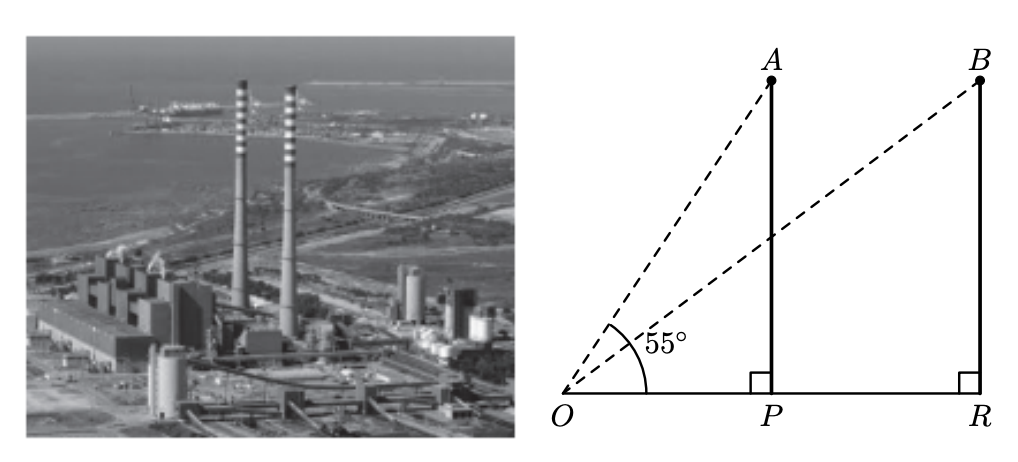
A figura da esquerda é uma fotografia dessa central termoelétrica e a figura da direita é uma representação das duas chaminés. A figura da direita não está desenhada à escala.

Na figura da direita, os segmentos de reta $[A P]$ e $[B R]$ correspondem às duas chaminés. O ponto $O$ corresponde a uma posição a partir da qual se observa o topo da chaminé representada por $[A P]$ segundo um ângulo com $55^{\circ}$ de amplitude.

Ambas as chaminés têm 225 metros de altura e a distância entre elas é igual a 132 metros.

Assim, relativamente à figura da direita, sabe-se que:

o ponto $P$ pertence ao segmento de reta $[O R]$
$A \hat{O P}=55^{\circ}$
$\overline{A P}=\overline{B R}=225 \mathrm{~m}$
$\overline{P R}=132 \mathrm{~m}$

Determina a amplitude do ângulo $B O R$.

Sugestão: Começa por determinar $\overline{O P}$.

Apresenta o resultado em graus, arredondado às unidades.

Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2016, 1ª Fase - Grupo Exercício 95

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários