Selecionar Exercício
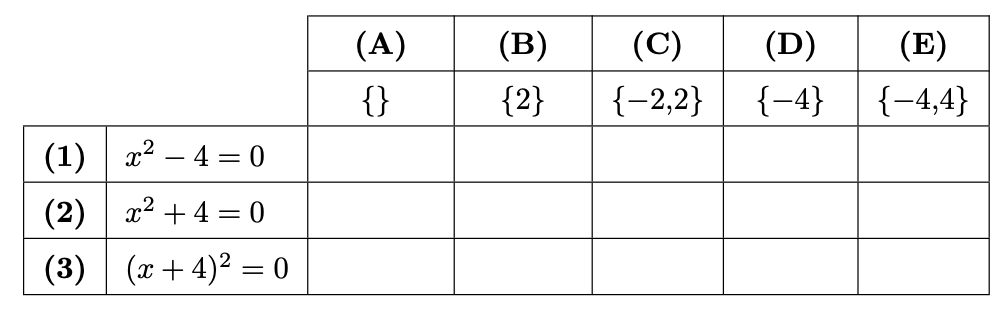
Para cada equação, (1), (2) e (3), assinala com $\mathbf{X}$ a opção que apresenta o respetivo conjunto solução.
Comentários
Mas não é impossível um número negativo ao quadrado dar um número negativo (refiro me à terceira alínea)?
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
não é isso que está lá escrito, tens de fazer a raiz quadrada do caso notável e do 0, que vai dar x+4=+/-0 trocas o quatro de lado e fica x=-4. Também podes verificar que ao substituires o -4 no x a equação vai ficar (-4+4)^2=0 <=> 0^2=0<=> 0=0, que é verdade
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para comentar, por favor inicia sessão ou cria uma conta.
