Mestre Panda

Dificuldade: díficil

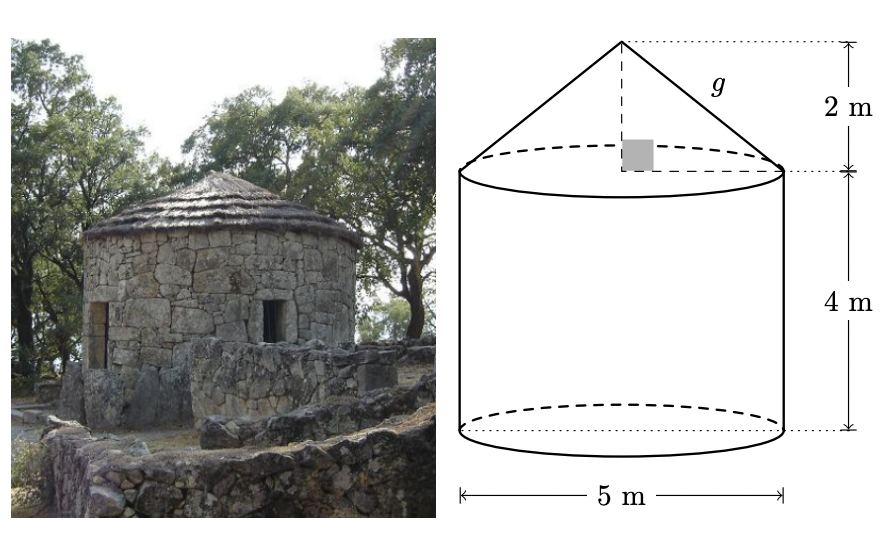
Na figura seguinte, à esquerda, está uma fotografia de uma casa castreja da Idade do Ferro, situada na Citânia de Briteiros.

A figura da direita representa um modelo geométrico dessa casa. Este modelo é um sólido que pode ser decomposto num cilindro reto e num cone reto.

Sabe-se que:

a base superior do cilindro coincide com a base do cone;
as bases do cilindro e a base do cone têm 5 metros de diâmetro;
o cilindro tem 4 metros de altura;
o cone tem 2 metros de altura.

O modelo não está desenhado à escala.

Calcula o volume do sólido representado na figura da direita.

Apresenta o resultado em metros cúbicos, arredondado às unidades. Se, nos cálculos intermédios, procederes a arredondamentos, conserva, pelo menos, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2023, Época Especial - Grupo 4 Exercício 6.2

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Rafaela Teixeira

Criado em 11/04/2025 15:37

6,25 arredondado às décimas é 6,3 e não 6,2.

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Lara Dinis rosa

Criado em 11/06/2025 08:55

Porque não fazem a conta do pi x 2,5^2?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários