Mestre Panda

Dificuldade: média

A Central Solar Fotovoltaica de Amareleja, no Alentejo, é uma das maiores do mundo. É constituída por dispositivos mecânicos seguidores solares (figura) - que suportam os painéis solares e os orientam para o Sol desde que este nasce até que se põe.

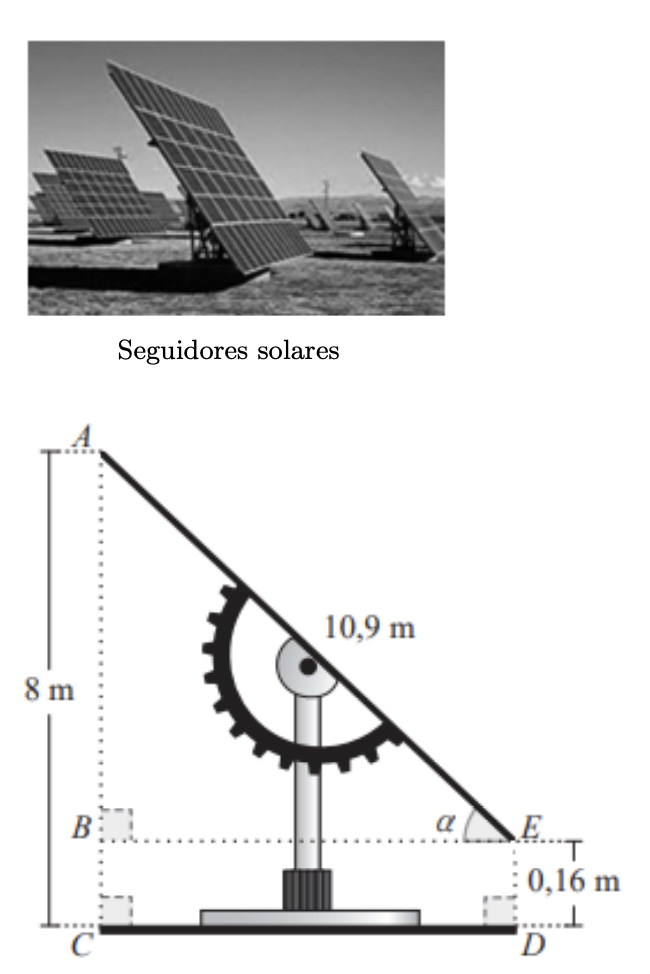
Na figura seguinte (em baixo), está representada, em esquema, uma vista lateral de um seguidor solar numa certa posição.

Nesse esquema, o painel solar está representado pelo segmento de reta $[A E]$.

Relativamente ao esquema, que não está desenhado à escala, sabe-se que:

o triângulo $[A B E]$ é retângulo em B;
$\overline{A E}=10,9 \mathrm{~m}$;
$A \hat{E} B=\alpha$
$[B C D E]$ é um retângulo;
$\overline{D E}=0,16 \mathrm{~m}$;
$\overline{A C}=8 \mathrm{~m}$;

Determina $\alpha$, a amplitude do ângulo de inclinação do painel solar em relação à horizontal.

Apresenta o resultado em graus, arredondado às unidades. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, três casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 85

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Leonor Sousa

Criado em 17/06/2025 10:25

Como é que descubro o ângulo se já sei o seno ?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários