Mestre Panda

Dificuldade: média

No Porto de Leixões, existe uma das maiores pontes basculantes do mundo.
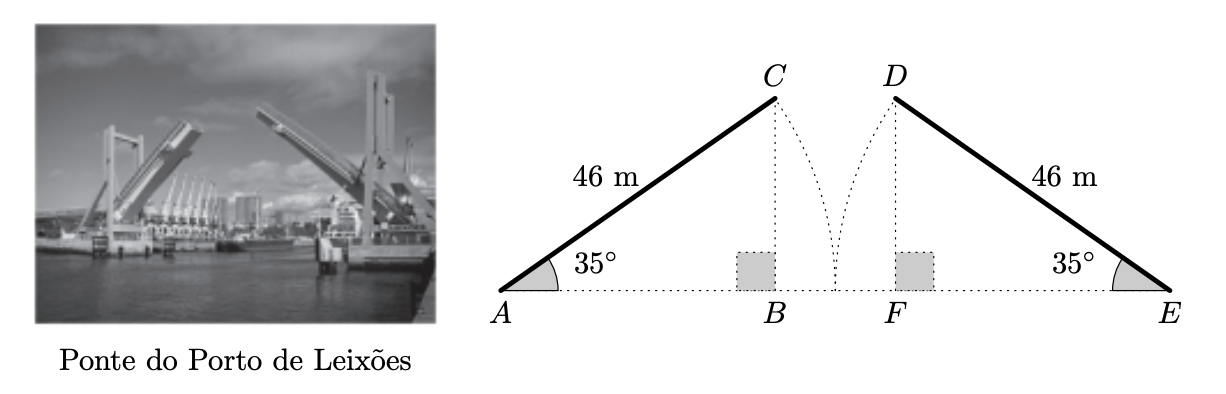
No esquema da figura seguinte, está representada a posição, em relação à horizontal, que as duas secções móveis da ponte tinham num certo instante. Nesse esquema, as seç̧ões móveis estão representadas pelos segmentos de reta $[A C]$ e $[E D]$.

Relativamente ao esquema, sabe-se que:

os triângulos $[A B C]$ e $[E F D]$ são retângulos nos vértices $B$ e $F$, respetivamente;
$\overline{A C}=\overline{E D}=46 \mathrm{~m}$;
$B \hat{A C}=D \hat{E} F=35^{\circ}$;
$\overline{A E}=\overline{A C}+\overline{E D}$.

Determina a distância entre os pontos $C$ e $D$, na posição representada no esquema da figura da direita.

Apresenta o resultado em metros, arredondado às unidades. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Sugestão: Começa por determinar $\overline{A B}$ ou $\overline{E F}$.

Fonte: Exame Matemática 3º Ciclo - 2018, 1ª Fase - Grupo Exercício 89

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários