Mestre Panda

Dificuldade: média

O João pratica kitesurf, desporto aquático em que se usa uma prancha e uma asa (semelhante a um paraquedas) comandada através de cabos.

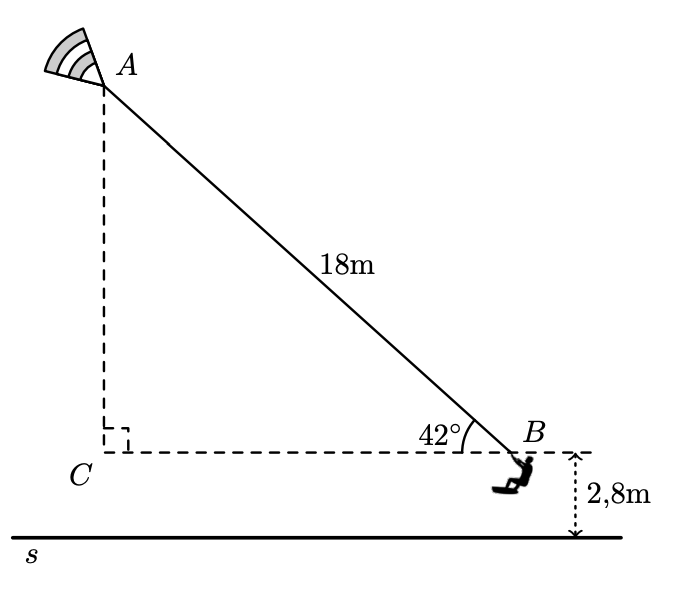
A figura ao lado é um esquema da situação em que o João se encontrava, num instante em que estava elevado em relação à superfície da água.

Relativamente ao esquema, sabe-se que:

a reta $s$ representa a superfície da água;
o segmento de reta $[A B]$ representa um dos cabos que liga a asa ao João;
as retas $B C$ e $s$ são paralelas;
a distância do ponto $B$ à reta $s$ é $2,8 \mathrm{~m}$;
$\overline{A B}=18 \mathrm{~m}$
$A \hat{B} C=42^{\circ}$ e $B \hat{C} A=90^{\circ}$.

O esquema não está desenhado à escala.

Determina a distância da asa à superfície da água, na situação representada na figura, ou seja, a distância do ponto $A$ à reta $s$.

Apresenta o resultado em metros, arredondado às décimas. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, três casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2019, 1ª Fase - Grupo Exercício 88

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários