Mestre Panda

Dificuldade: díficil

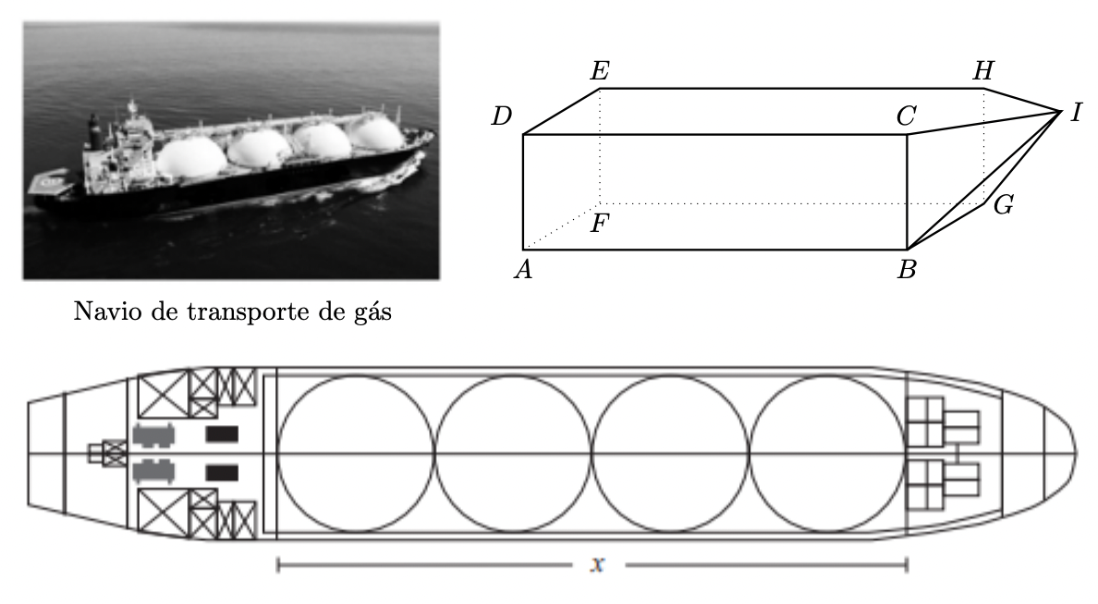
No transporte marítimo de gás, usam-se, frequentemente, navios com tanques esféricos.

Na figura seguinte, à direita, está representado, em esquema, o casco de um desses navios.

Este esquema é composto pelo paralelepípedo retângulo $[A B C D E F G H]$ e pela pirâmide retangular irregular $[B C H G I]$, cujo vértice $I$ pertence ao plano que contém a face $[C D E H]$ do paralelepípedo retângulo.

Na figura em baixo, está representada a vista de cima de um navio de transporte de gás.

Admite que os quatro tanques esféricos:

têm o mesmo raio e espessura desprezável;
estão colocados num compartimento com a forma de um paralelepípedo retângulo, encostados uns aos outros e às paredes do compartimento, sem que sejam deformados;
têm, cada um, $33750 \mathrm{~m}^{3}$ de volume.

Determina o comprimento do compartimento onde estão colocados os quatro tanques esféricos, designado por $x$ na figura anterior.

Apresenta o valor pedido em metros, arredondado às unidades. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, duas casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2018, 1ª Fase - Grupo Exercício 871

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários