Mestre Panda

Dificuldade: média

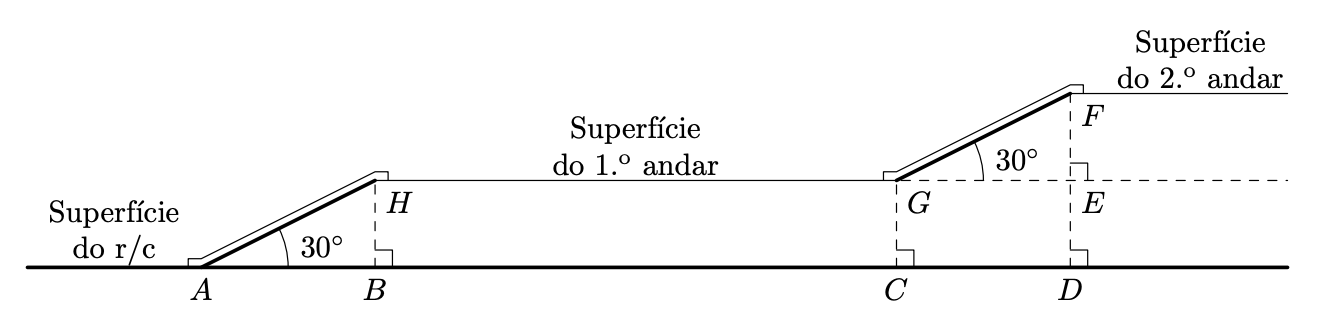
Na figura seguinte, apresenta-se o esquema de uma estrutura de três pisos onde serão montadas duas escadas rolantes, uma entre o rés do chão e o $1 .^{\circ}$ andar e outra entre o $1 .^{\circ}$ andar e o $2 .^{\circ}$ andar.

Sabe-se que:

$\overline{A D}=23 \mathrm{~m}$
$\overline{B C}=12 \mathrm{~m}$
$\overline{A B}=\overline{C D}$
$B \hat{A} H=E \hat{G} F=30^{\circ}$

A figura não está desenhada à escala.

Determina $\overline{D F}$, ou seja, determina a distância da superfície do rés do chão à superfície do $2 .^{\circ}$ andar.

Apresenta o valor pedido em metros, arredondado às centésimas.

Se procederes a arredondamentos nos cálculos intermédios, conserva pelo menos três casas decimais. Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2017, 1ª Fase - Grupo Exercício 93

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários