Mestre Panda

Dificuldade: média

A primeira figura é uma fotografia da Central Fotovoltaica do Alto Rabagão, em Montalegre. Esta central produz energia elétrica solar a partir de painéis fotovoltaicos assentes numa plataforma flutuante.

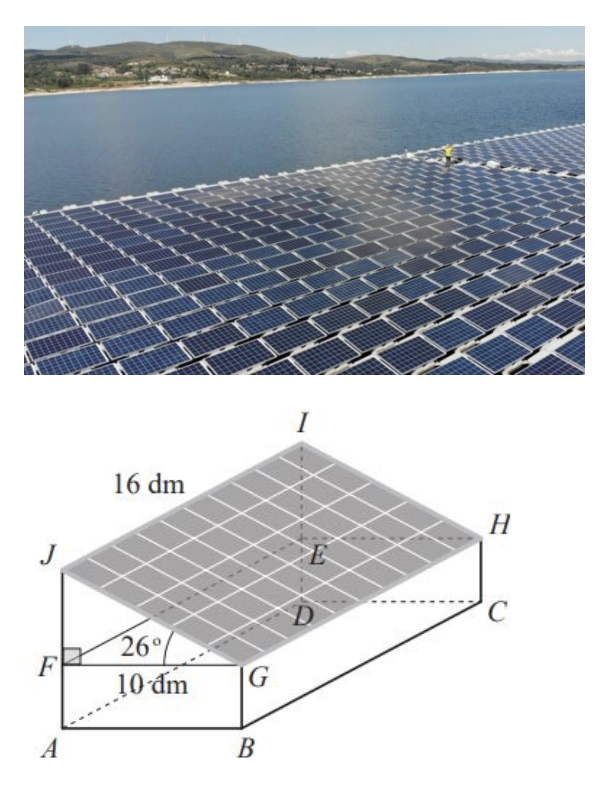
Na figura seguinte está representado um modelo geométrico de um painel fotovoltaico e do respetivo flutuador.

O modelo é constituído pelo paralelepípedo retângulo $[A B C D E F G H]$, que representa o flutuador, pelo retângulo $[G H I J]$, que representa o painel fotovoltaico, e pelos segmentos de reta $[F J]$ e $[E I]$, que representam as hastes que suportam o painel fotovoltaico. Relativamente à figura em baixo, sabe-se que:

o triângulo $[J F G]$ é retângulo em $F$;
$\overline{F G}=10 \mathrm{dm}$;
$\overline{I J}=16 \mathrm{dm}$;
$J \hat{G} F=26^{\circ}$.

O modelo não está desenhado à escala.

Determina a área do painel fotovoltaico, representado na figura de baixo pelo retângulo $[G H I J]$.

Apresenta o resultado em decímetros quadrados, arredondado às unidades. Se, nos cálculos intermédios, procederes a arredondamentos, conserva, pelo menos, três casas decimais.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2022, 1ª Fase - Grupo Exercício 82

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Mariana Pereira

Criado em 09/06/2024 20:14

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários