Mestre Panda

Dificuldade: média

Algumas camas são articuladas, ou seja, têm uma secção que pode ser inclinada.

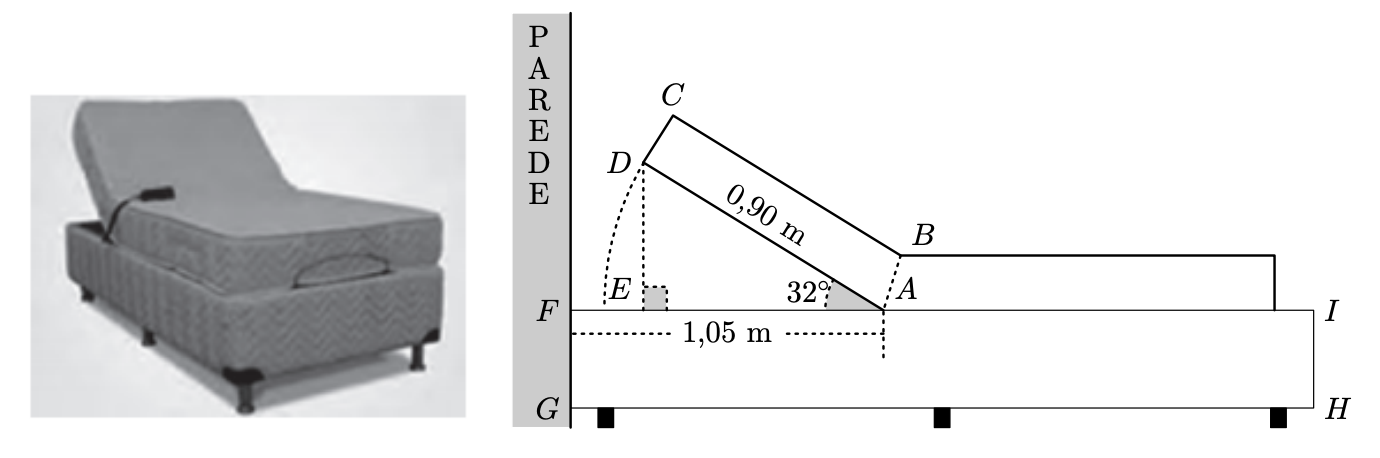
No esquema da figura seguinte, está representada a vista lateral de uma cama articulada, com o topo encostado a uma das paredes de um quarto. Nesse esquema, o trapézio $[A B C D]$ representa a secção inclinada da cama e o retângulo $[F G H I]$ representa a base da cama.

Relativamente ao esquema, que não está à escala, sabe-se que:

os pontos $A$ e $E$ pertencem ao segmento de reta $[F I]$;
o triângulo $[A D E]$ é retângulo no vértice $E$;
$\overline{A D}=0,9 \mathrm{~m}$ e $\overline{A F}=1,05 \mathrm{~m}$;
$D \hat{A} E=32^{\circ}$

Determina a distância do vértice $D$ à parede do quarto, na posição representada no esquema da figura.

Apresenta o resultado em metros, arredondado às centésimas. Se procederes a arredondamentos nos cálculos intermédios, conserva, pelo menos, três casas decimais.

Apresenta todos os cálculos que efetuares.

Sugestão: Começa por determinar $\overline{A E}$.

Fonte: Exame Matemática 3º Ciclo - 2018, 1ª Fase - Grupo Exercício 91

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Ana Reis

Criado em 08/06/2024 12:36

A distancia da parede a D não serias Ex2?Já que pelo o que podemos observar a distancia da parede a E é metade da distancia de D à parede

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários