Mestre Panda

Dificuldade: díficil

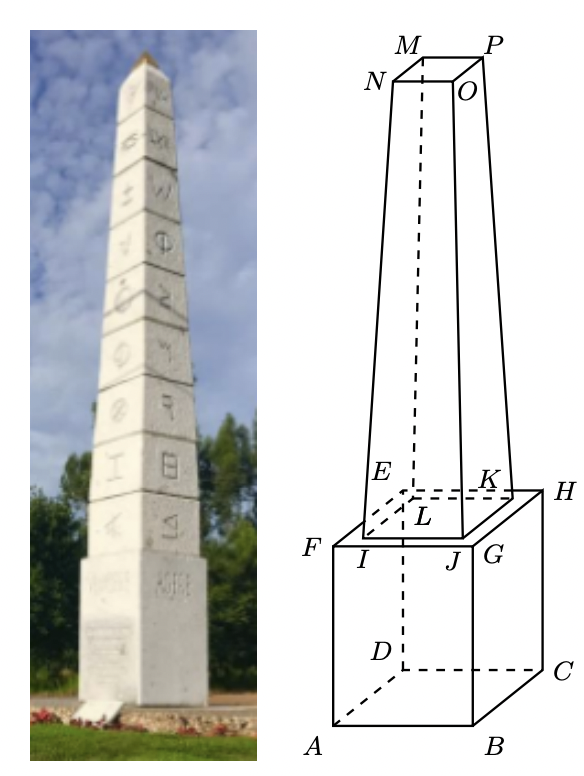
A figura seguinte é uma fotografia de um obelisco de granito maciço, obra do escultor vimaranense Dinis Ribeiro, que foi construído para homenagear a comunidade educativa da freguesia de Ponte, em Guimarães.

Na figura da direita, está representado um modelo geométrico do obelisco. Este modelo é constituído por um prisma quadrangular reto $[A B C D E F G H]$ e por um tronco de pirâmide $[I J K L M N O P]$ de bases quadradas.

Sabe-se que:

o prisma $[A B C D E F G H]$ tem bases quadradas com 1,4 metros de aresta e tem 1,8 metros de altura;
o tronco de pirâmide $[I J K L M N O P]$ tem 4,5 metros de altura e é o tronco de uma pirâmide reta com 18 metros de altura;
$\overline{N O}=0,9 \mathrm{~m} ;$
$\overline{I J}=1,2 \mathrm{~m}$.

O modelo geométrico não está desenhado à escala.

Determina o volume do obelisco cujo modelo geométrico está representado na figura mais à direita.

Apresenta o resultado em metros cúbicos, arredondado às unidades. Nos cálculos intermédios não deves proceder a arredondamentos.

Apresenta todos os cálculos que efetuares.

Fonte: Exame Matemática 3º Ciclo - 2021, 1ª Fase - Grupo Exercício 867

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários