Mestre Panda

Dificuldade: díficil

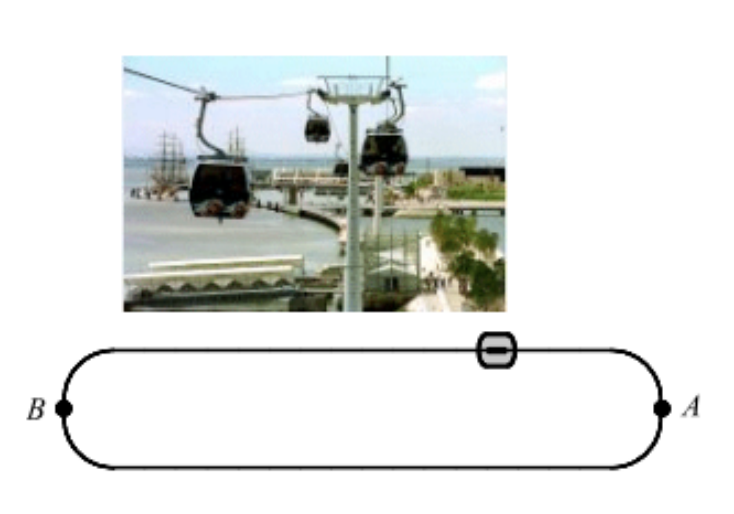
Na fotografia, em cima, podes ver o teleférico do Parque das Nações.

Na figura de baixo, está representado um esquema do circuito (visto de cima) efetuado por uma cabina do teleférico.

No teleférico do Parque das Nações, o número de cabinas em utilização não é sempre o mesmo, mas duas cabinas consecutivas estão sempre igualmente espaçadas.

O ajuste da distância entre as cabinas é feito automaticamente, de acordo com a seguinte fórmula,

$$n \times c=3$$
em que:

$c$ representa a distância, em quilómetros, entre duas cabinas consecutivas;

$n$ é o número total de cabinas em utilização.

Quando o teleférico está em funcionamento, a sua velocidade média pode variar entre 11 e 17 quilómetros por hora.

Qual é o maior número possível de voltas completas que uma cabina pode dar durante uma hora? Justifica a tua resposta, começando por referir o significado da constante 3 na fórmula $n \times c=3$.

Fonte: Exame Matemática 3º Ciclo - 2006, 1ª Fase - Grupo Exercício 301

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários