Mestre Panda

Dificuldade: díficil

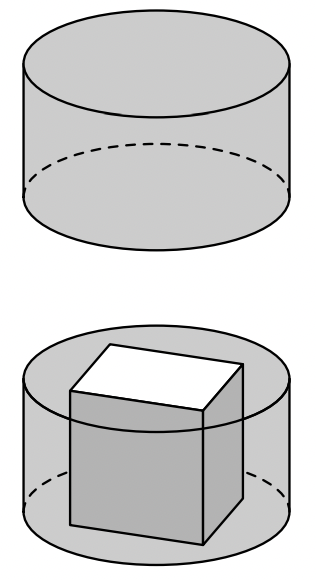
Na figura seguinte, à esquerda, está representado um recipiente cilíndrico que se encheu com um líquido colorido. Nesse líquido, mergulhou-se um cubo cuja aresta é igual à altura do cilindro. Tal como a figura seguinte, à direita sugere, o cubo ficou assente na base do recipiente.

Admite que:

a aresta do cubo mede $6 \mathrm{~cm}$
o raio da base do cilindro mede $5 \mathrm{~cm}$

Quando se mergulhou o cubo no recipiente, uma parte do líquido transbordou.

Determina o volume do líquido que ficou no recipiente depois de nele se ter mergulhado o cubo (figura em baixo).

Apresenta o resultado em $\mathrm{cm}^{3}$, arredondado às unidades. Apresenta todos os cálculos que efetuares.

Nota - Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo, duas casas decimais.

Fonte: Exame Matemática 3º Ciclo - 2013, 1ª Fase - Grupo Exercício 888

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Escreve a tua resposta aqui:

Comentários