Imagem do exercício
Num laboratório, um grupo de alunos pretende titular, com rigor, uma solução aquosa de hidróxido de sódio, $\mathrm{NaOH}(\mathrm{aq})$, utilizando uma solução-padrão de ácido clorídrico, $\mathrm{HCl}(\mathrm{aq})$, de concentração $0,280 \mathrm{~mol} \mathrm{~dm}^{-3}$. A reação que ocorre pode ser traduzida por
$$\mathrm{HCl}(\mathrm{aq})+\mathrm{NaOH}(\mathrm{aq}) \rightarrow \mathrm{NaCl}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{O}(\mathrm{I})$$
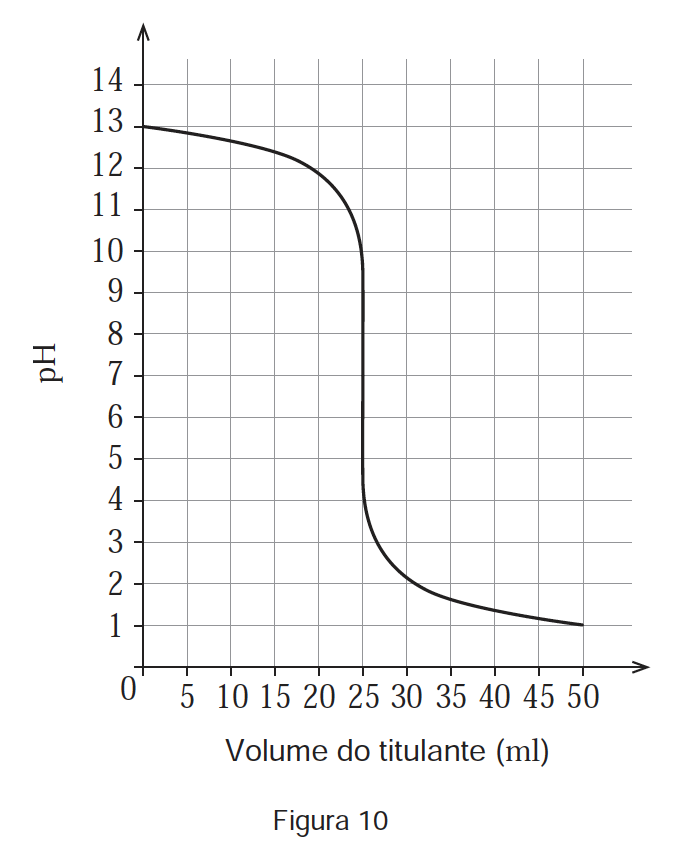
Uma solução aquosa de $80,0 \mathrm{ml}$ de $\mathrm{NaOH}\left(M=40,00 \mathrm{~g} \mathrm{~mol}^{-1}\right)$ foi preparada a partir de uma amostra impura do reagente sólido, da qual se gastou $1,20 \mathrm{~g}$. Retiraram-se $20,0 \mathrm{~ml}$ dessa solução e titulou-se esta quantidade de solução com a solução-padrão de $\mathrm{HCl}$, tendo-se obtido a curva de titulação representada na Figura 10.
Admita que as impurezas são inertes.
Calcule a massa de impurezas na amostra inicial de $\mathrm{NaOH}$.
Apresente todos os cálculos efetuados.
Fonte: IAVE
Fonte: IAVE
1) Leitura, no gráfico, o volume de titulante gasto no ponto de equivalência.
Até atingir o ponto de equivalência, ou seja, o ponto onde as quantidades estequiométricas estão de acordo com a equação química, foram titulados $25 \mathrm{~mL}$.
2) Cálculo da quantidade de $\mathrm{NaOH}$ que reage até se atingir o ponto de equivalência.
$25 \mathrm{~mL}$ de ácido clorídrico de concentração $0,280 \mathrm{~mol} \mathrm{~dm}^{-3}$ representa uma quantidade de $n=c V \quad 0,025 \times 0,280=7,00 \times 10^{-3} \mathrm{~mol}$
3) Cálculo da quantidade de $\mathrm{NaOH}$ puro que existe em $80 \mathrm{~mL}$ de solução.
Como a estequiometria é $1: 1$, existe, em $20 \mathrm{~mL}$ de solução de $\mathrm{NaOH}, 7,00 \times 10^{-3} \mathrm{~mol}$, pelo que em $80 \mathrm{~mL}$ existem $0,0280 \mathrm{~mol}$.
4) Cálculo da massa de impurezas.
$0,0280 \mathrm{~mol}$ de $\mathrm{NaOH}$ representa $0,0280 \times 40,00=1,12 \mathrm{~g}$. Assim, existem $1,20-1,12=0,08 \mathrm{~g}$ de impurezas.
Fonte: Lucas Campos
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para comentar, por favor inicia sessão ou cria uma conta.
